はじめに

集めたデータ分布のバラつきを確認する際に、便利なものが標準偏差です。平均値だけではわからない平均との偏差値が簡単に確認できるため、対策や改善などに活用できます。
この記事では、Excelで標準偏差の値を求める際に使用する関数と、標準偏差の求め方、データを利用したグラフの作成方法などをご紹介します。

標準偏差とは？

標準偏差とは、集めたデータが平均値からどれくらいのブレがあるか、数値で示したものです。テスト結果やアンケート結果などの平均値は、全体の合計を集めたデータの数で割ることで簡単に割り出せます。しかし、集めたデータの平均値が同じでも、実際のデータ値と平均値がかけ離れているケースもあるため、どれくらいの違いがあるかを確認することが大切です。

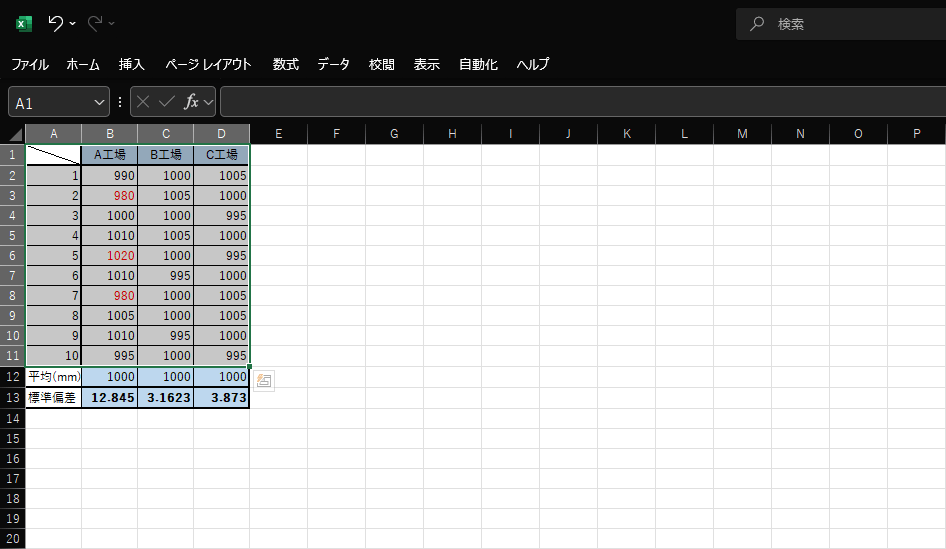
たとえば、複数の工場で製作している製品があるとします。製品サイズの平均は1mで、平均との誤差が10mm以内は許容範囲内です。

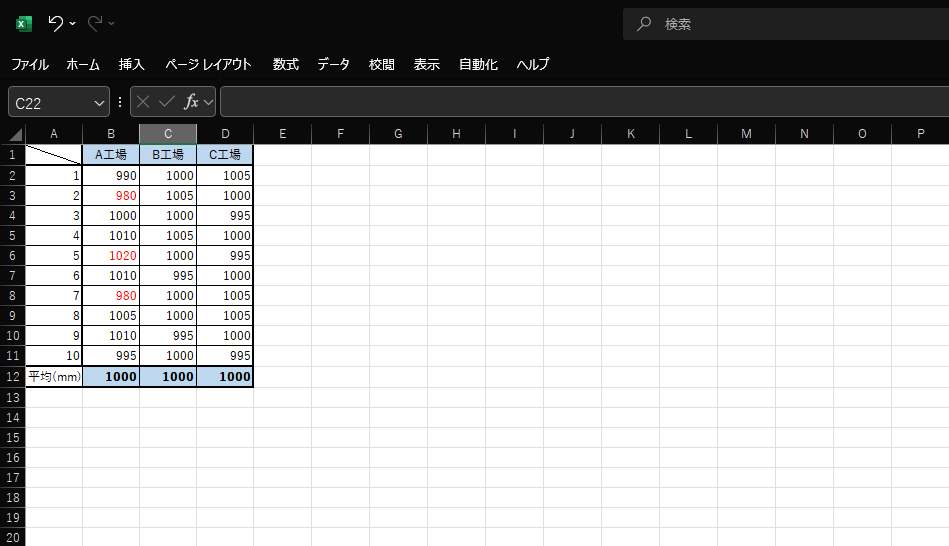
3つの工場で製作した製品のサイズ平均は1000mm、つまり1mですが、A工場では誤差が10mmを超えた製品が3つあります。B工場とC工場の誤差は許容範囲内ではありますが、B工場では誤差が少なく、C工場では誤差が多く発生しています。表にまとめられた結果から、B工場で製作している製品が優良品であり、A工場では品質改善の見直しが、C工場では誤差を減らせるような取り組みが必要とわかるでしょう。
このように、平均値だけでは判断できない場合に、データの値を分析・確認できるものが「標準偏差」です。

母集団・標本とは

母集団は「調査・研究の対象となる全体の集まり」のことで、標本は「母集団から選び出した一部の集まり」のことです。

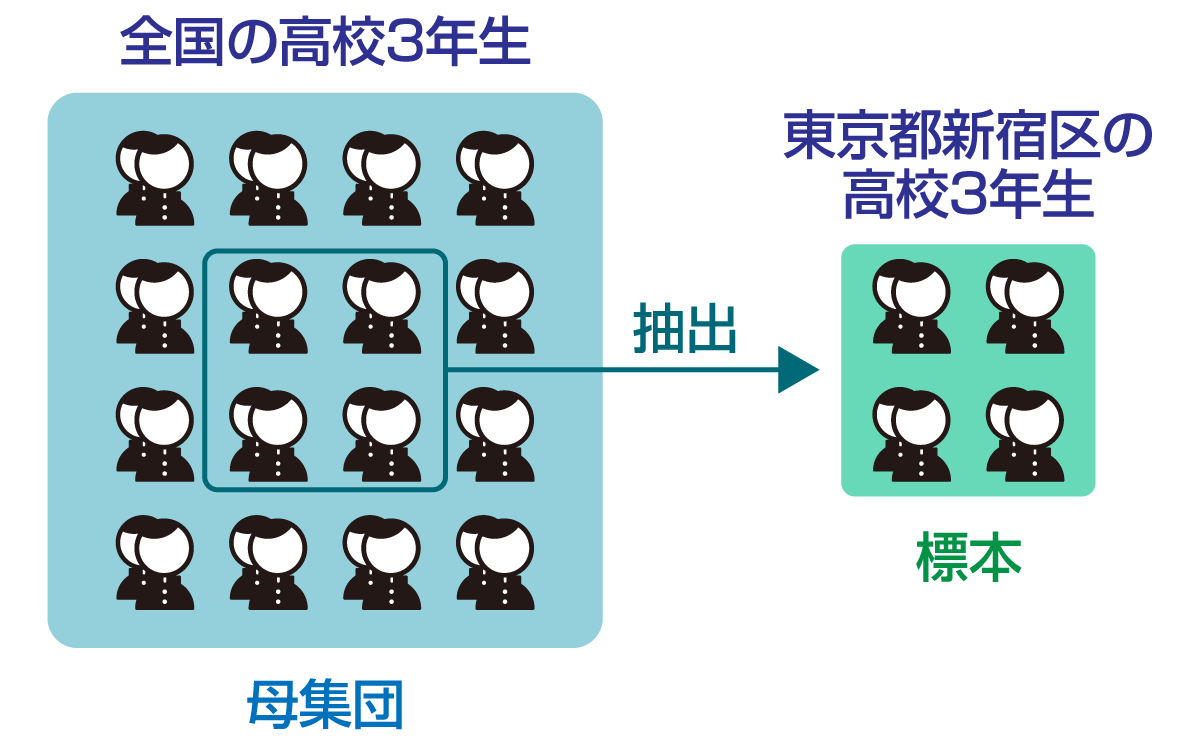
標準偏差を求める際は、母集団全体のデータを使用することが理想的ですが、実際には対象やデータ総量が多すぎるといった理由から、難しいケースもあります。そういった場合は、母集団からデータの一部を標本として選び、その標本の標準偏差を計算します。計算結果を確認することで、母集団全体のデータにどれくらいバラつきがあるか推測できるでしょう。

標準偏差をExcel関数で求めてみよう

標準偏差は、Excel関数を使用することで簡単に求められます。使用する関数は2つあります。

• STDEV.P関数
• STDEV.S関数

関数それぞれの違いや使い方について、簡単にご紹介します。

STDEV.P関数

STDEV.P関数は「母集団全体のデータから標準偏差を求める」際に使用する関数です。たとえば、工場で製作している製品のクオリティチェックをする際に使用できます。実際に製作した製品と製品の基準値を比較して、どれくらいの誤差があるかが確認できれば、必要な品質改善に取り組みやすくなるでしょう。
実際の入力画面を参考に、手順をご紹介します。

1．標準偏差を入力したいセルを選択して、セル内に「=STDEV.P」と入力します。参考画像の表ではB13です。

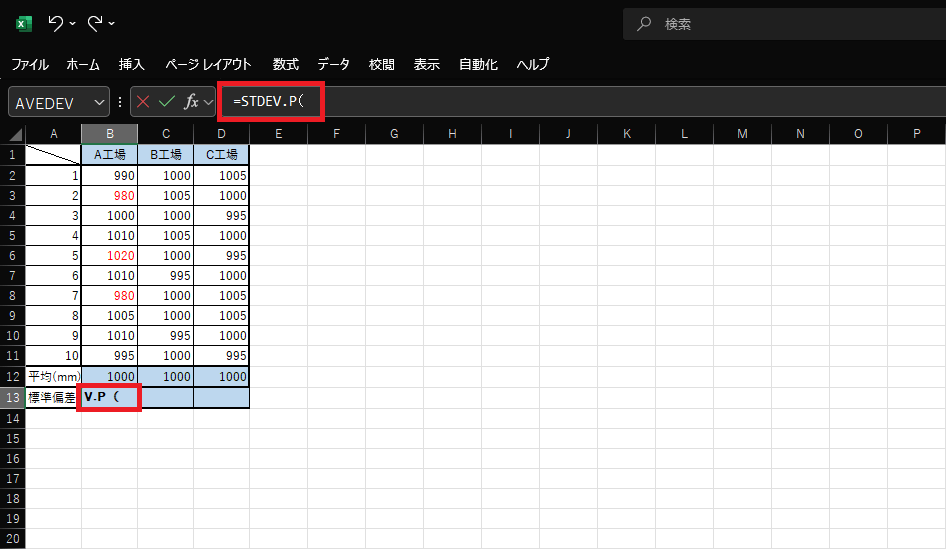
2．参考にする範囲、引数を指定します。参考画像の表ではB2からB11をドラッグして選択します。
直接入力する際は「B2:B11」ではなく「(B2:B11)」となるように入力しましょう。

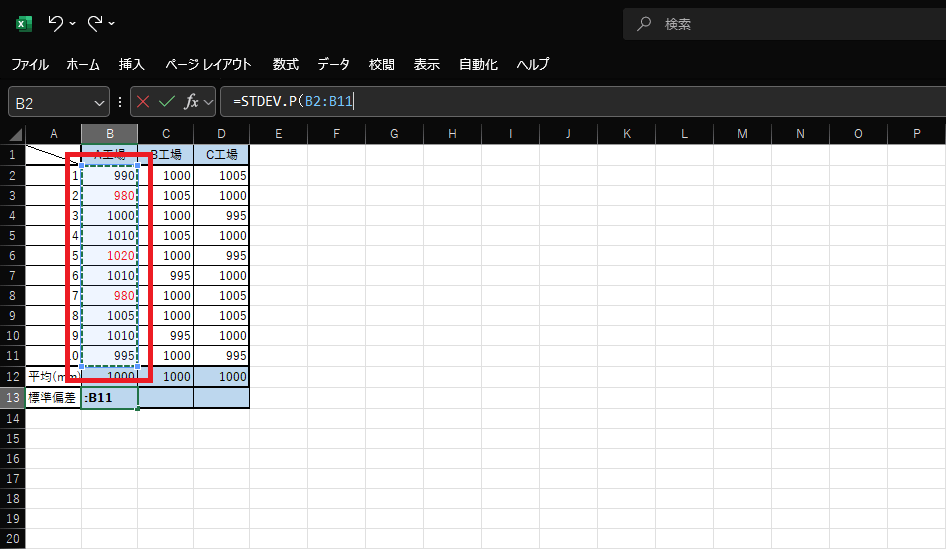
入力後にEnterキーを押すと、A工場の標準偏差が求められます。

3．A工場の標準偏差が入力されたセル（B13）を選択し、オートフィル機能で右にドラッグします。

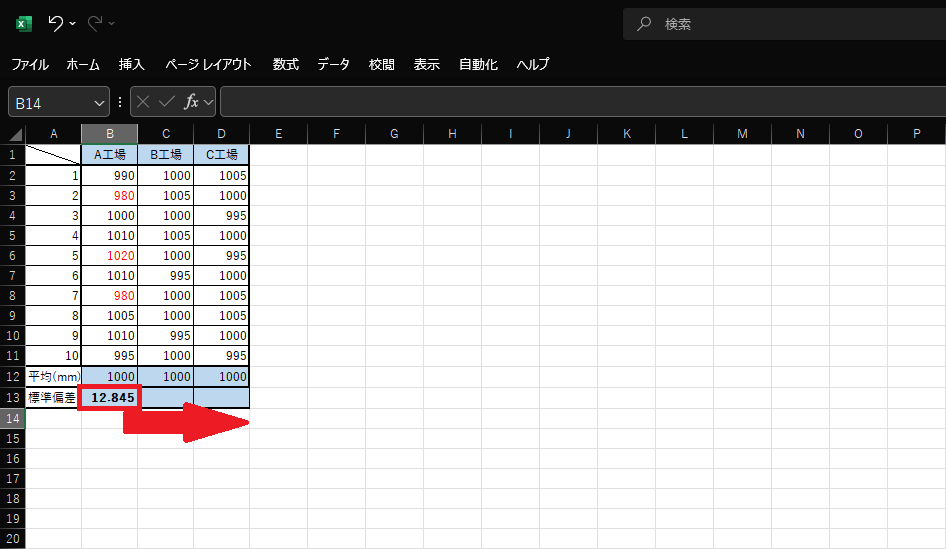
4．すべての標準偏差を求めた表ができました。

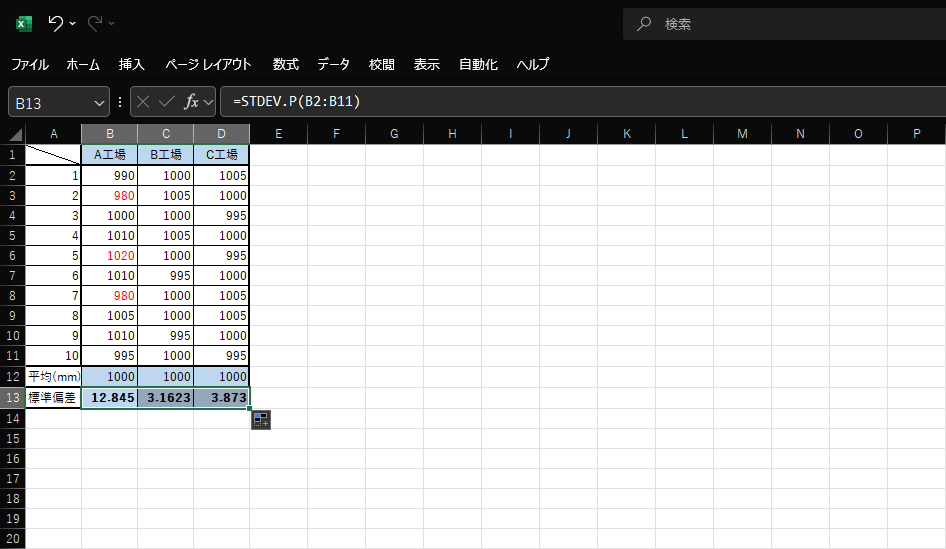
STDEV.S関数

STDEV.S関数は、母集団全体を調べることが難しい場合に「抽出した標本から母集団の標準偏差値を推定する」ために使用する関数です。STDEV.S関数を使用すれば、標本から算出した標準偏差値を元として「母集団における標準偏差」を求められます。
関数の入力方法は、STDEV.P関数と同じです。

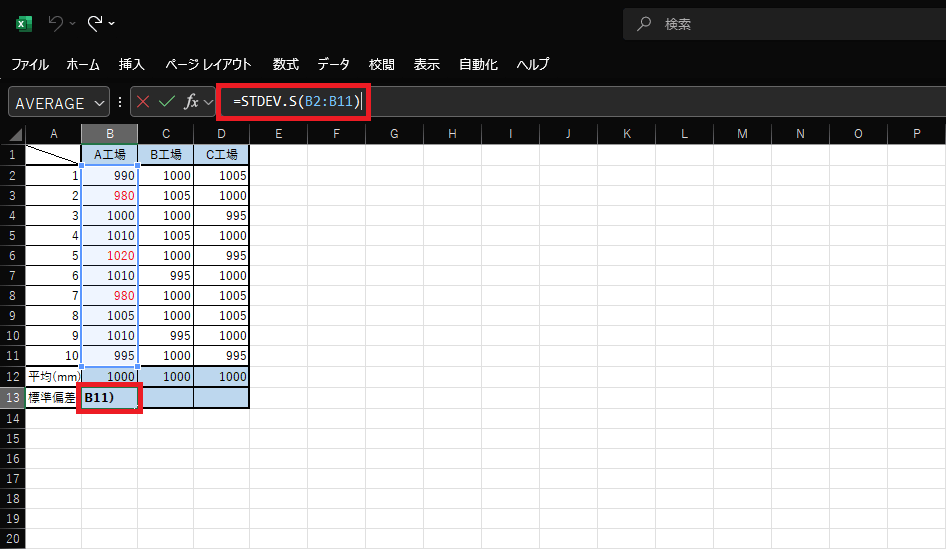
ただし、母集団全体ではなく、無作為に抽出した標本を対象とするため、算出される値は推定値となります。そのため、同じ表データを使用した場合でも「STDEV.P」で求めた標準偏差の結果より値が大きくなるケースもあります。
以下の画像は、同じ値をSTDEV.P関数とSTDEV.S関数を使用して、それぞれ標準偏差を求めたものです。

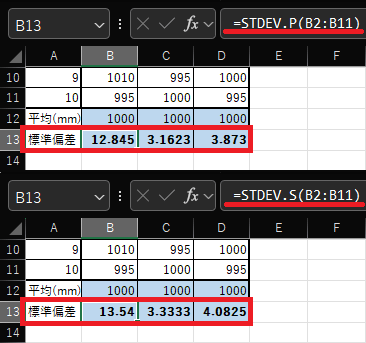
ご覧いただいたように、同じ表データを使用していても算出される推定値には差が出ます。使用するデータが同じ場合は、どちらの関数を使用しているかわからなくならないよう、注意しましょう。

STDEVP関数/STDEV関数について

「STDEVP関数/STDEV関数」は、どちらもExcel2010以前のバージョンで使用できる関数であり、それぞれ「STDEV.P関数/STDEV.S関数」と同様の使い方ができます。
バージョンが違っても使い方に大きな差はありませんので、前項でご紹介した方法を参考にしてください。

• Excel2010以降のバージョンで使用できる

• STDEV.P関数

• STDEV.S関数

• Excel2010以前のバージョンで使用できる

• STDEVP関数

• STDEVS関数

標準偏差をExcelでグラフにする方法とは？

標準偏差は、Excelで簡単にグラフ化できます。求めた標準偏差をグラフにまとめると、視覚的に見やすくなるでしょう。
Excel関数を活用して標準偏差をグラフにする方法を2つ、ご紹介します。

1．散布図にする方法

散布図は、データの分布状況を可視化し、把握しやすくするグラフです。2つのデータの関係性を素早く把握し、改善策や計画立案を効率的に進めたいときに活用できます。

1．散布図にしたい表から、データ範囲を選択します。この時、平均値や標準偏差まで選択しないよう、注意しましょう。
参考画像ではA1からD11がデータ範囲です。

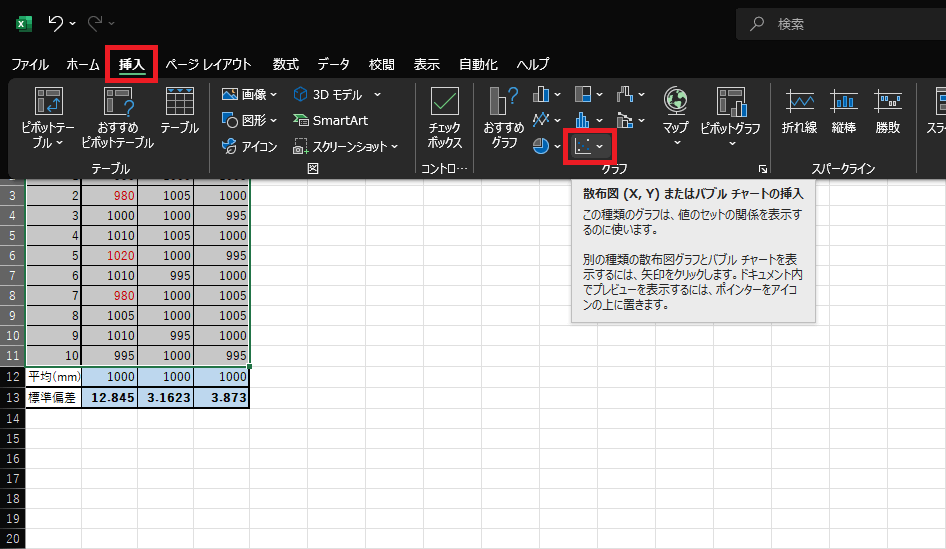
2．『挿入』タブのグラフ内から「散布図またはバブルチャートの挿入」を選択します。いくつかの丸い点が、枠内に散らばっているアイコンが目印です。

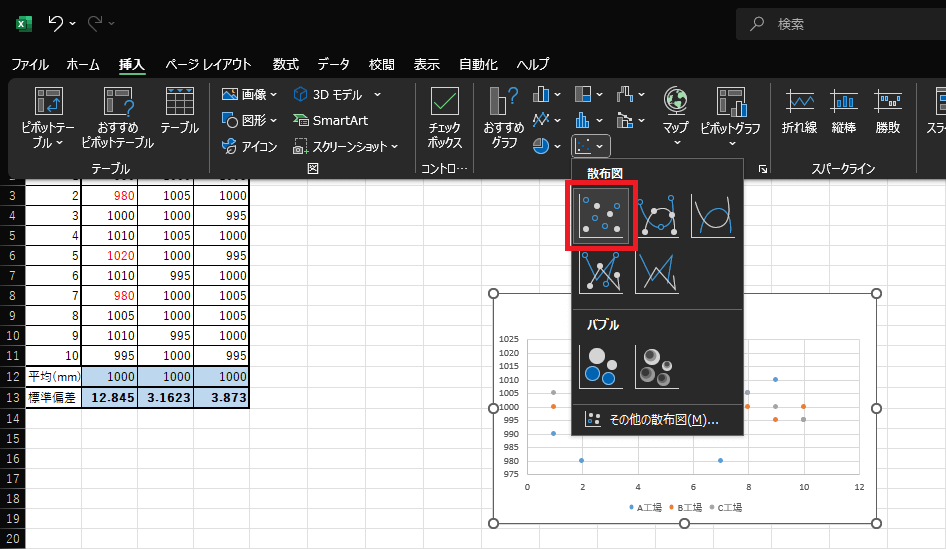
3．開かれたタブ内の左上、丸がばらばらに配置されているアイコンをクリックします。

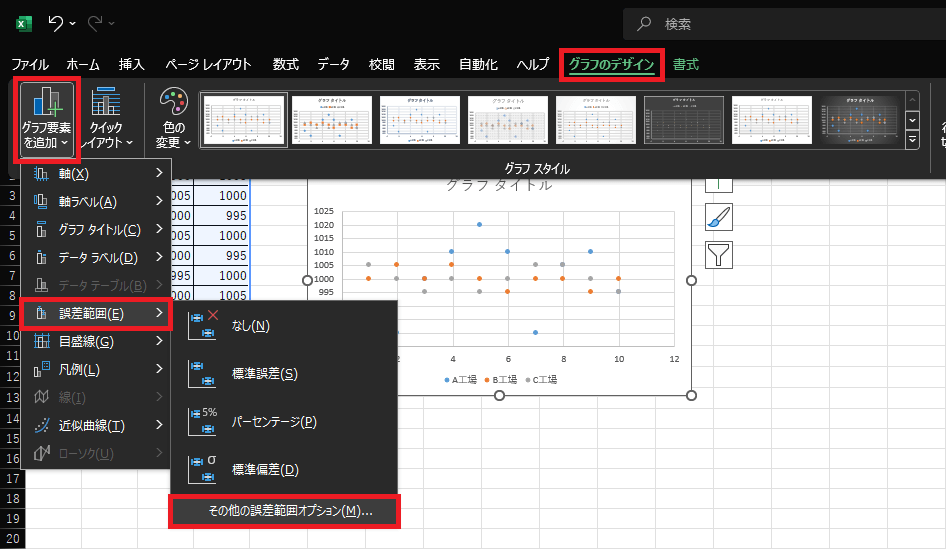
4．散布図が表示されたら『グラフのデザイン』タブを開きます。
「グラフ要素を追加」⇒「誤差範囲」⇒「その他の誤差範囲オプション」の順に選択します。

再び選択肢が表示されたら「A工場」を選択します。

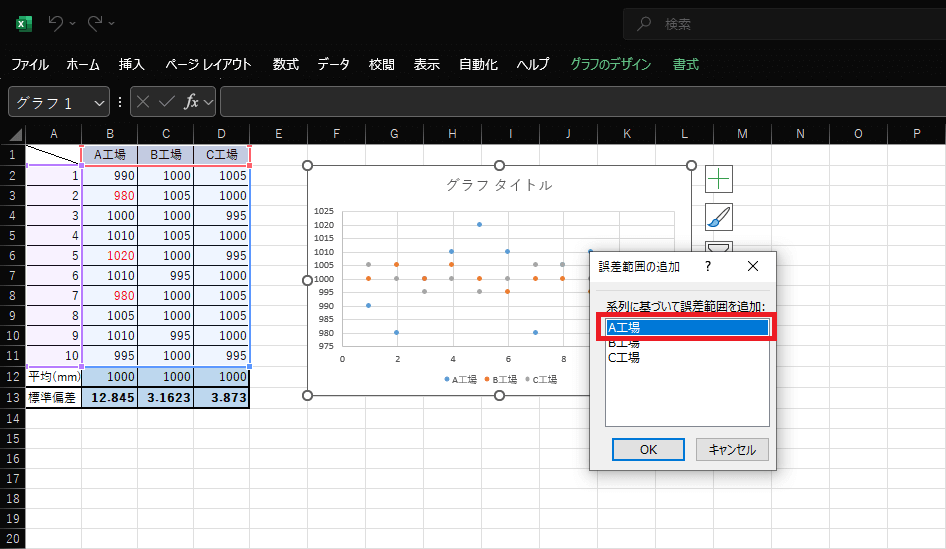
5．Excel画面の右側に「誤差範囲の書式設定」が開いたら、一番下までスクロールして「ユーザー設定」の選択と、右横の「値の設定」をクリックします。

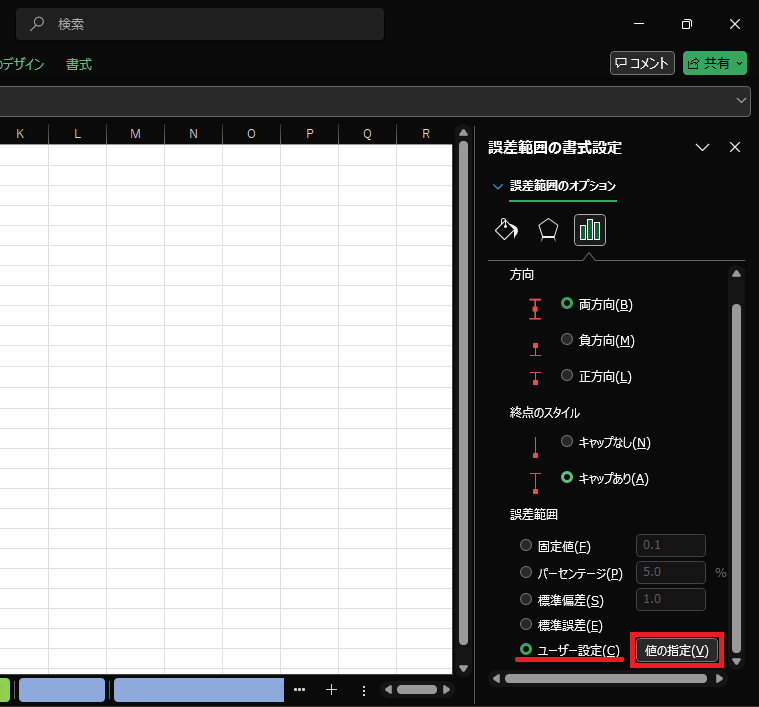
6．開かれた「ユーザー設定の誤差範囲」の入力欄に、標準偏差の値を入力します。正の誤差、負の誤差、どちらも同じ値で問題ありません。

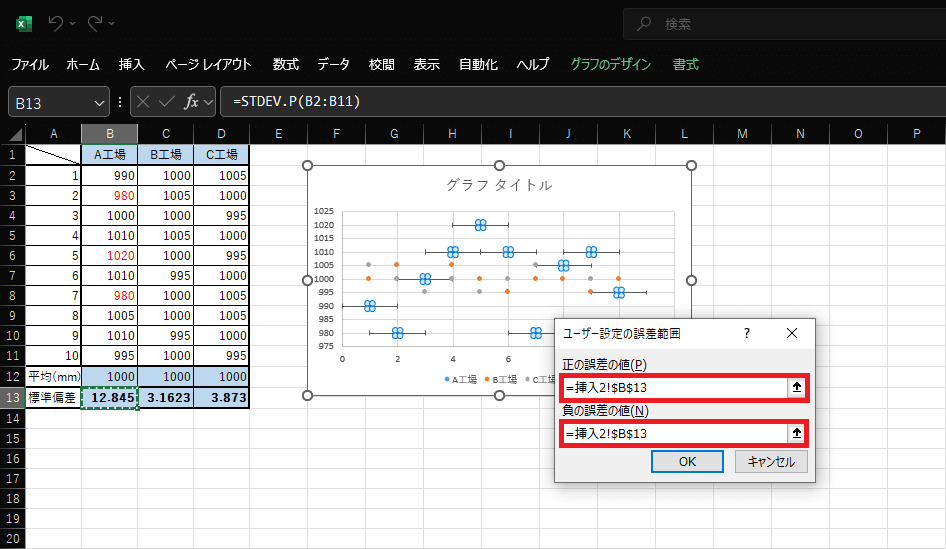
OKをクリックすると、グラフに誤差範囲が表示されます。

7．表示された誤差範囲のうち、水平に伸びている線をクリックします。

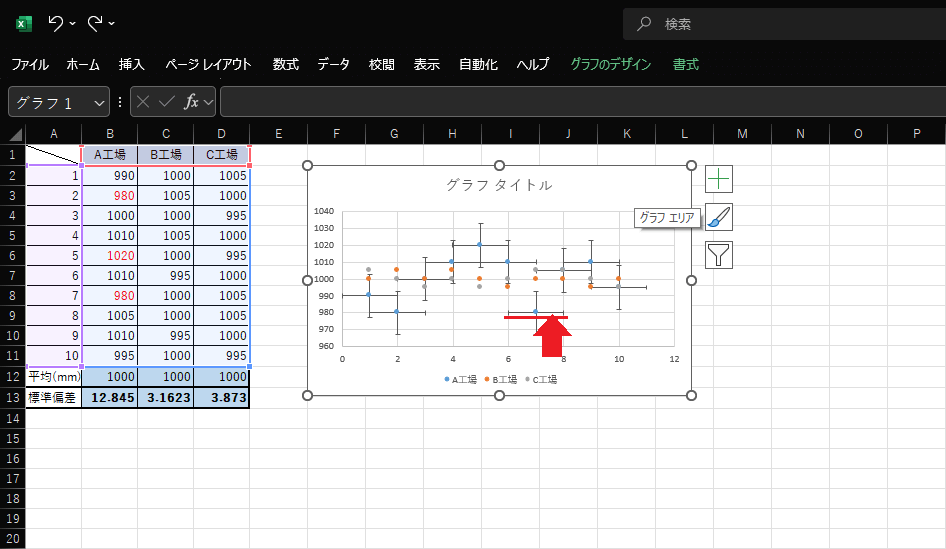
画像のように水平の線が選択できたら、Deleteキーを押します。

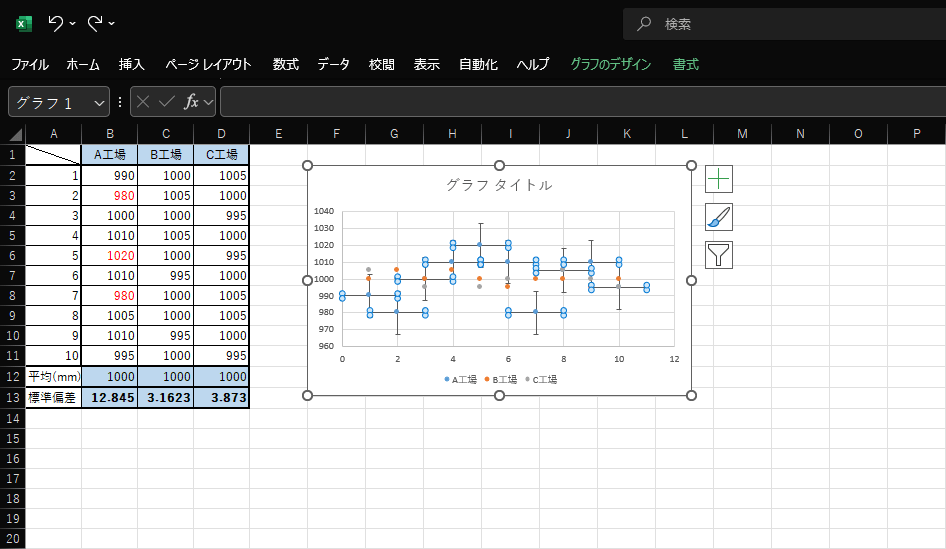
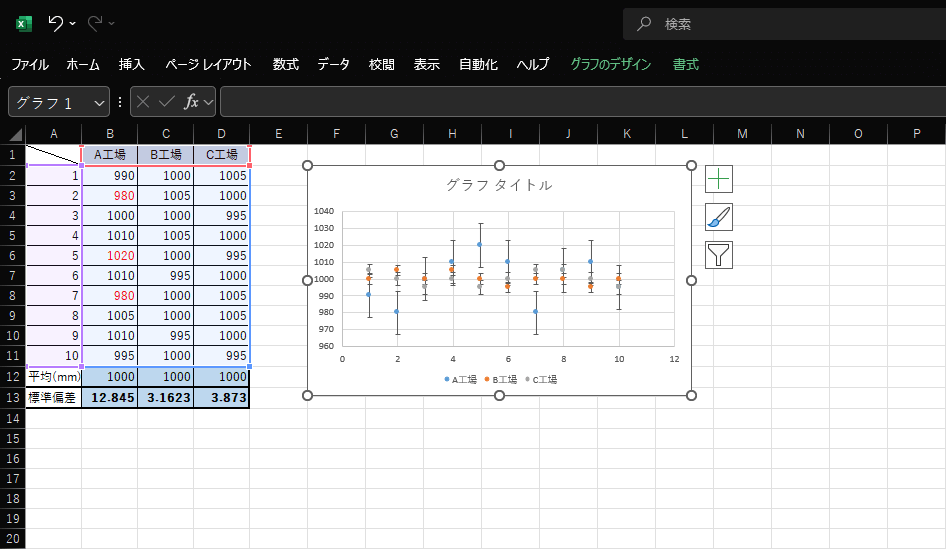
8．B工場、C工場も同じように入力すると、誤差範囲が表示された散布図が作成できます。

2．棒グラフにする方法

棒グラフは、データの差異が可視化しやすくなるグラフです。作成した棒グラフに、標準偏差を元にしたエラーバーを付けることで、データの誤差範囲が把握しやすくなります。テストやアンケートなど、集めたデータのバラつきを確認する際に活用できます。

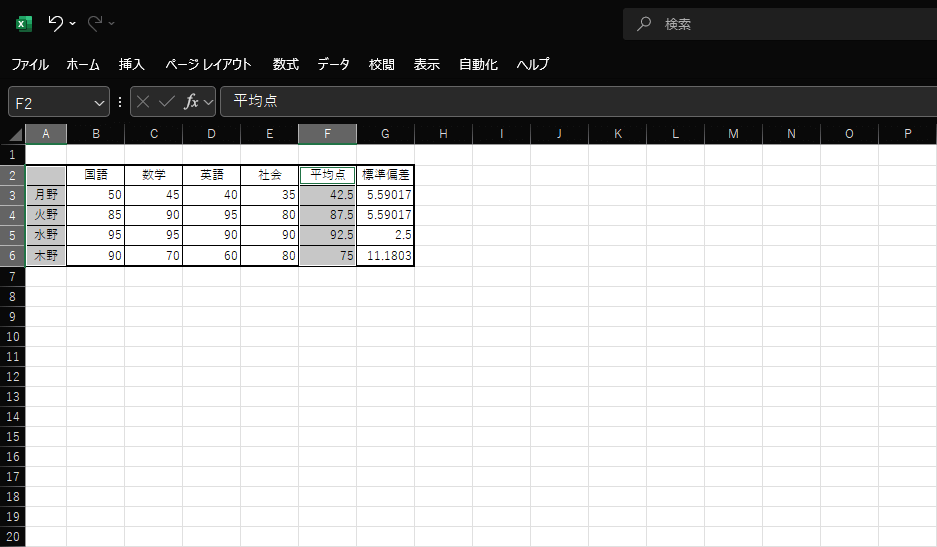
1．棒グラフにしたい表から、対象と平均点を選択します。
参考画像の対象はA2からA6で、平均点はF2からF6です。

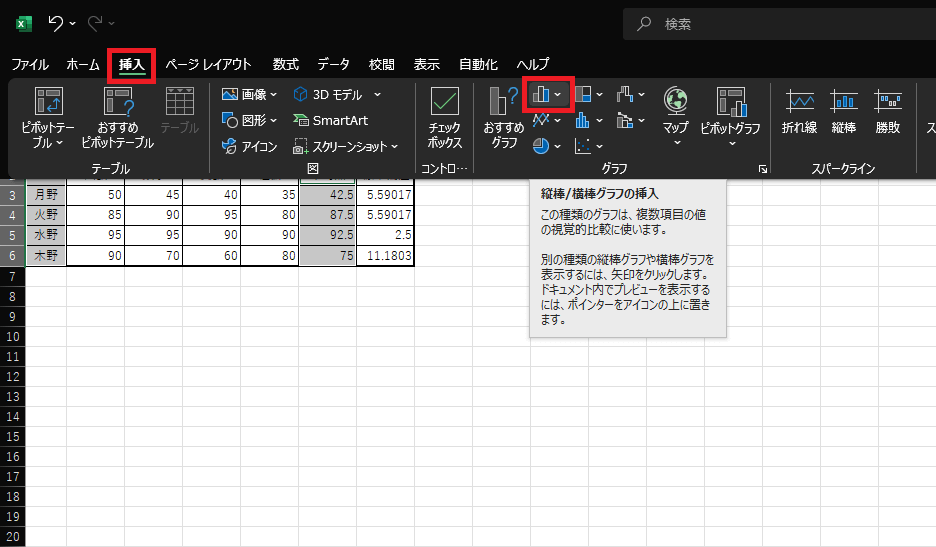
2．『挿入』タブのグラフ内から「縦棒/横棒グラフの挿入」を選択します。色の違う棒グラフが、3本並んでいるアイコンが目印です。

3．「2D縦棒」を選択します。本記事では左端のグラフを選択して進めます。

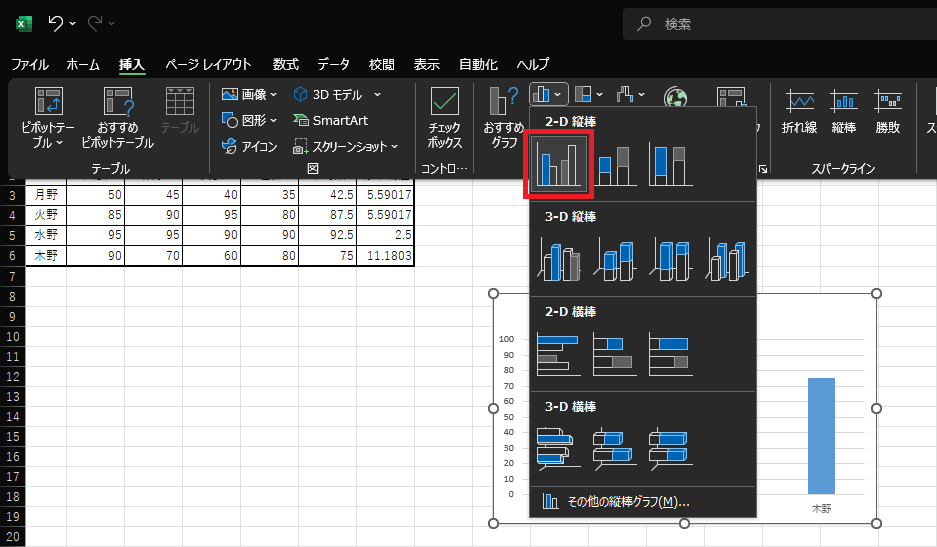
4．棒グラフが表示されたら『グラフのデザイン』タブを開きます。
「グラフ要素を追加」⇒「誤差範囲」⇒「その他の誤差範囲オプション」の順に選択します。

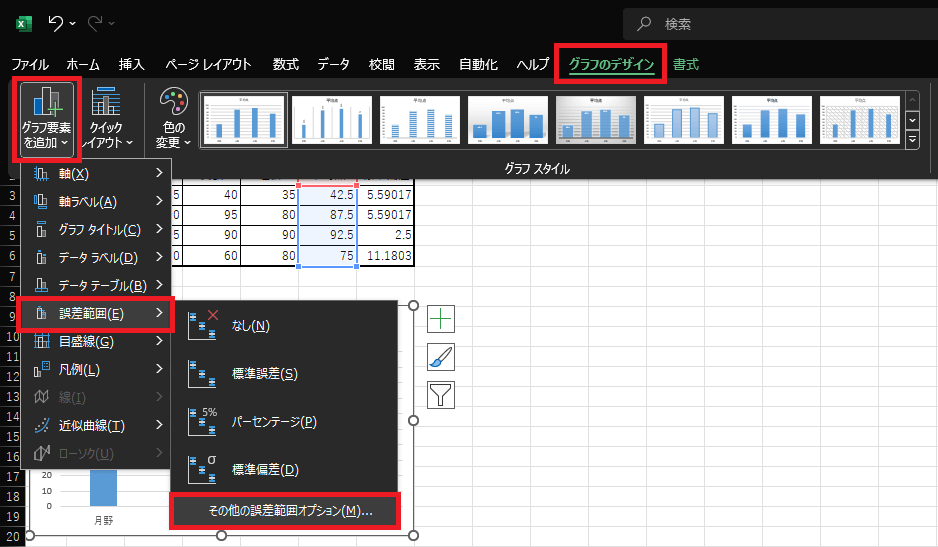
5．Excel画面の右側に「誤差範囲の書式設定」が開いたら、一番下までスクロールして「ユーザー設定」の選択と、右横の「値の設定」をクリックします。

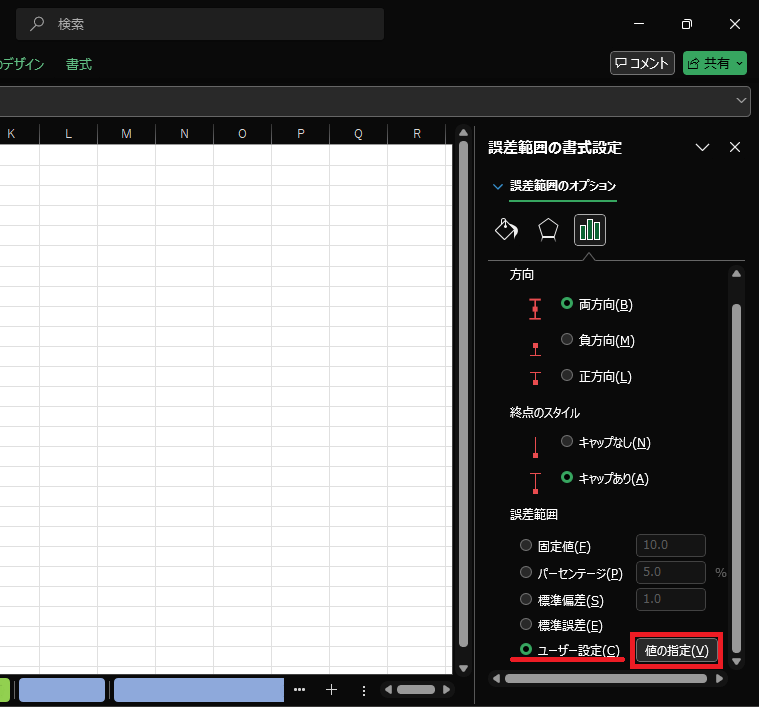
6．開かれた「ユーザー設定の誤差範囲」の入力欄に、標準偏差の値を入力します。正の誤差、負の誤差、どちらも同じ値で問題ありません。

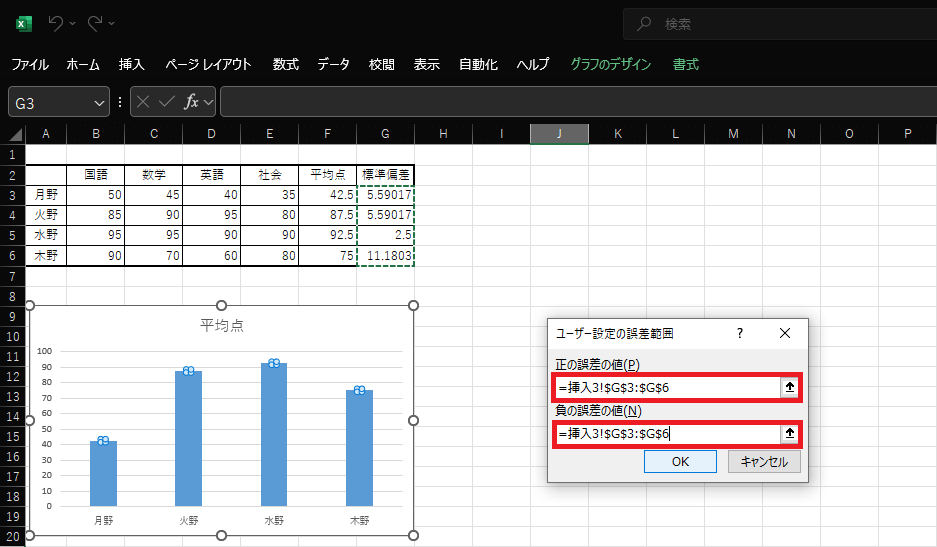
入力欄を選択して、G3からG6をドラッグすることで、簡単に入力できます。

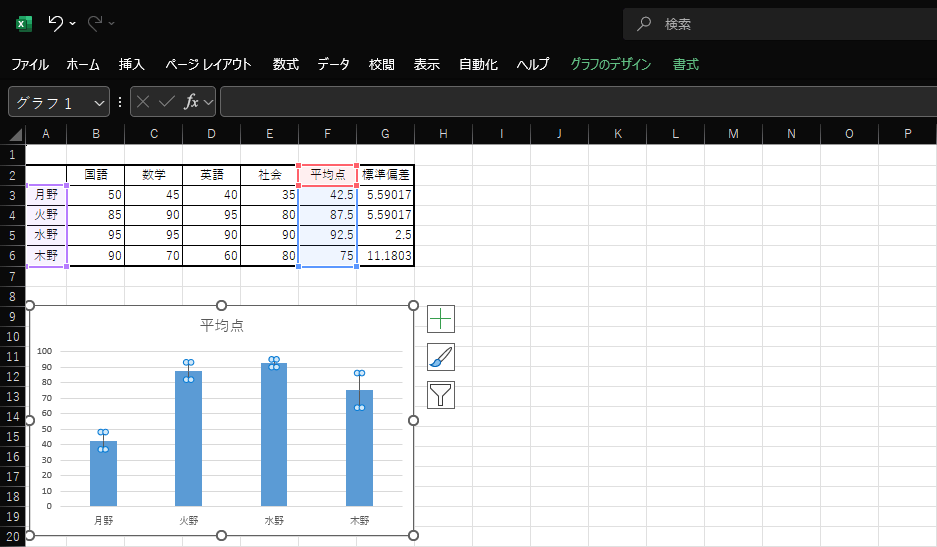
7．エラーバーつきの棒グラフが作成できました。エラーバーの幅が、誤差範囲の大きさを示しています。

まとめ

標準偏差はデータの平均値からのバラつきを示す指標です。同じ平均値を持つデータを使用していても、バラつき具合は異なる場合があるため、標準偏差を計算してデータのバラつき具合を確認することが重要です。ExcelではSTDEV.P関数とSTDEV.S関数を使用して標準偏差が簡単に計算できます。これらの関数を適切に使い分けることで、母集団または標本のデータ分布を効率的に求められるでしょう。
また、求めた標準偏差は、そのままExcelでのグラフ作成に利用できます。二つの標準偏差関数を活用することで、データの分布状況を視覚的に理解しやすく表現するのに役立つでしょう。